この記事は測度論の勉強記録です。
間違い等あれば記事下部のコメントフォームからコメントで教えて頂けると幸いです。
※この記事は作成中です。上方連続性、下方連続性の証明はまだ着手していません。
参考にした or 勉強している本
「測度・確率・ルベーグ積分 応用への最短コース」(原 啓介)という本で勉強しています。
定義 1.9 測度・測度空間
可測空間\( S, M \)に対し、\(M\)上で定義された関数\(\mu\)が以下の性質を満たすとき、\(\mu\)を\(S, M\)上の測度という。
性質1
任意の\( A \in M \)に対し、\( 0 \leq \mu(A) \leq \infty \)。特に\( \mu(\emptyset) = 0 \)
性質2
\( A_1, A_2, \cdots \in M \)が非交差的ならば
$$
\mu \left( \bigsqcup_{n=1}^\infty A_n \right) = \sum_{n=1}^\infty \mu(A_n)
$$
性質2はσ-加法性という。
この\( S, M, \mu \)の組\( (S, M, \mu) \)を測度空間という。
定理 1.3 測度の簡単な性質
上記の本の定理 1.3について解説します。
まずは、性質を列挙します。その後、1つずつ説明していきます。
測度空間\( (S, M, \mu) \)について以下が成立。
有限加法性
\( A_1, \cdots, A_n \in M \)が非交差的ならば
$$
\mu \left( \bigsqcup_{i=1}^n A_i \right) = \sum_{i=1}^n \mu(A_i)
$$
単調性
\( A_1, A_2 \in M \)について
$$
A_1 \subset A_2 \ ならば \ \mu(A_1) \leq \mu(A_2)
$$
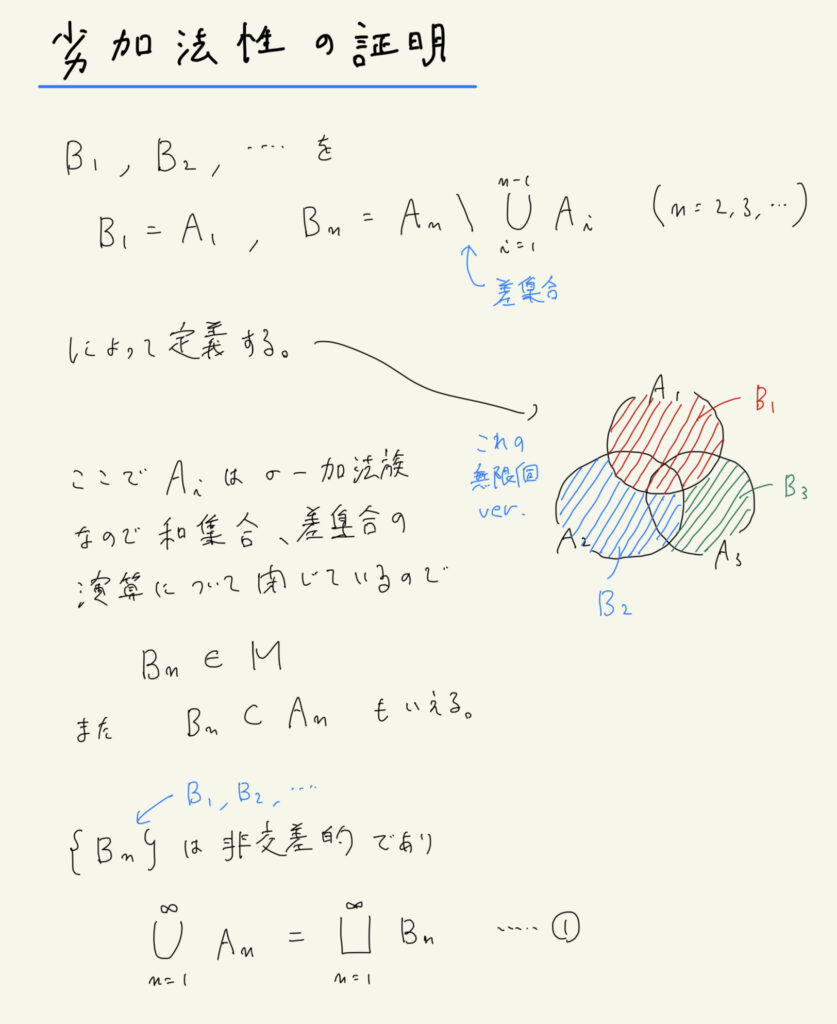
劣加法性
\( A_1, A_2, \cdots \in M \)について
$$
\mu \left( \bigcup_{n=1}^\infty A_n \right) \leq \sum_{n=1}^\infty \mu(A_n)
$$
上方連続性
\( A_1, A_2, \cdots \in M \)が単調に増大、つまり\( A_1 \subset A_2 \subset \cdots \)ならば
$$
\lim_{n \to \infty} \mu(A_n) = \mu \left( \bigcup_{n=1}^\infty A_n \right)
$$
下方連続性
\( A_1, A_2, \cdots \in M \)が単調に減少、つまり\( A_1 \supset A_2 \supset \cdots \)で、さらに\( \mu(A_1) \lt \infty \)ならば
$$
\lim_{n \to \infty} \mu(A_n) = \mu \left( \bigcap_{n=1}^\infty A_n \right)
$$
性質の説明
有限加法性


単調性

劣加法性





コメント