正定値行列・負定値行列・半正定値行列・半負定値行列

$$
\newcommand{\bs}{\boldsymbol}
\newcommand{\der}{\partial}
\newcommand{\defeq}{\overset{\text{def}}{=}}
$$

この記事はなるべく間違いの無いように気を付けて書きましたが、間違いなどあればコメントフォームからコメントで教えて頂けると幸いです。

普通の線形代数の本にはあまり書かれていないのに、統計や機械学習の勉強をしていると突然出てくる「正定値行列」「負定値行列」「半正定値行列」「半負定値行列」について解説します。

これらは対称行列に対して定義されます。対称行列とは次の条件を満たす行列のことです。

$$
A^T = A
$$

$ A^T $はAの転置行列です。この定義から対称行列になれるのは行数、列数が等しい正方行列に限られることが分かります。

正定値行列

Aをn次の対称行列、$ \bs{x} $をn次元縦ベクトルとします。このとき

$$
f(\bs{x}) = \bs{x}^T A \bs{x}
$$

を2次形式と言います。

2次形式はいかつい見た目をしていますが、下の画像のようにスカラーになります。

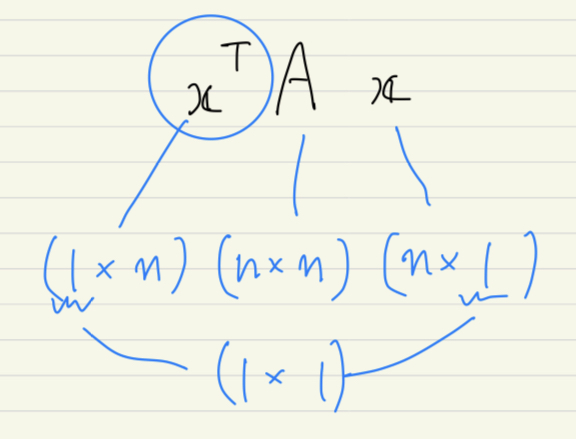
$ \bs{0} $（零ベクトル）を除く任意の縦ベクトル$ \bs{x} $に対して

$$
\bs{x}^T A \bs{x} \gt 0
$$

を満たすとき、対称行列Aを正定値行列という。

零ベクトルでない、どんなベクトルでサンドイッチしても値が0より大きくなるということです。

注意すべき点は、これは行列の性質であって、行列Aが正定値と表現します。

半正定値行列は簡単です。安心してください。

単純に先程の条件$ \bs{x}^T A \bs{x} \gt 0 $が緩まって以下の条件になるだけです。

$ \bs{0} $（零ベクトル）を除く任意の縦ベクトル$ \bs{x} $に対して

$$
\bs{x}^T A \bs{x} \geq 0
$$

これらは先程の正定値行列と半正定値行列について、値が負になるだけです。

一応示しておきます。

$ \bs{0} $（零ベクトル）を除く任意の縦ベクトル$ \bs{x} $に対して

$$
\bs{x}^T A \bs{x} \lt 0
$$

を満たすとき、対称行列Aを負定値行列という。

$ \bs{0} $（零ベクトル）を除く任意の縦ベクトル$ \bs{x} $に対して

$$
\bs{x}^T A \bs{x} \leq 0
$$

を満たすとき、対称行列Aを半負定値行列という。

他のサイトで2次形式$ \bs{x}^T A \bs{x} $を内積の記号で紹介しているサイトがありました。

ベクトル$ \bs{a} $と$ \bs{b} $の内積を$ \langle \bs{a}, \bs{b} \rangle $と表す場合、2字形式は以下のように表せます。

$$
\bs{x}^T A \bs{x} = \langle A \bs{x}, \bs{x} \rangle = \langle \bs{x}, A \bs{x} \rangle
$$

内積を行列の流儀で計算する変換の公式として次があります。

かなり必須の覚えておくべき公式です。

内積を$ \langle \bs{a}, \bs{b} \rangle $と表す場合

$$
\langle \bs{a}, \bs{b} \rangle = \bs{a}^T \bs{b}
$$

※転置は$ \bs{a} $に適用されています。

内積が普通にドットで表されている場合は次のようになります。

$$
\bs{a} \cdot \bs{b} = \bs{a}^T \bs{b}
$$