ポアソン分布の確率分布は次のようになる。
\( \lambda > 0 \)として
$$
f(x) = \frac{e^{-\lambda} \lambda^x}{x!} \qquad x=0, 1, 2, \cdots
$$
ポアソン分布のパラメータは\( \lambda \)だけである。
確率変数Xがポアソン分布\( Po(\lambda) \)に従う時、期待値、分散は次のようになる。
$$
E(X) = \lambda
$$
$$
V(X) = \lambda
$$
これをモーメント母関数を用いて証明する。
以下手書き。


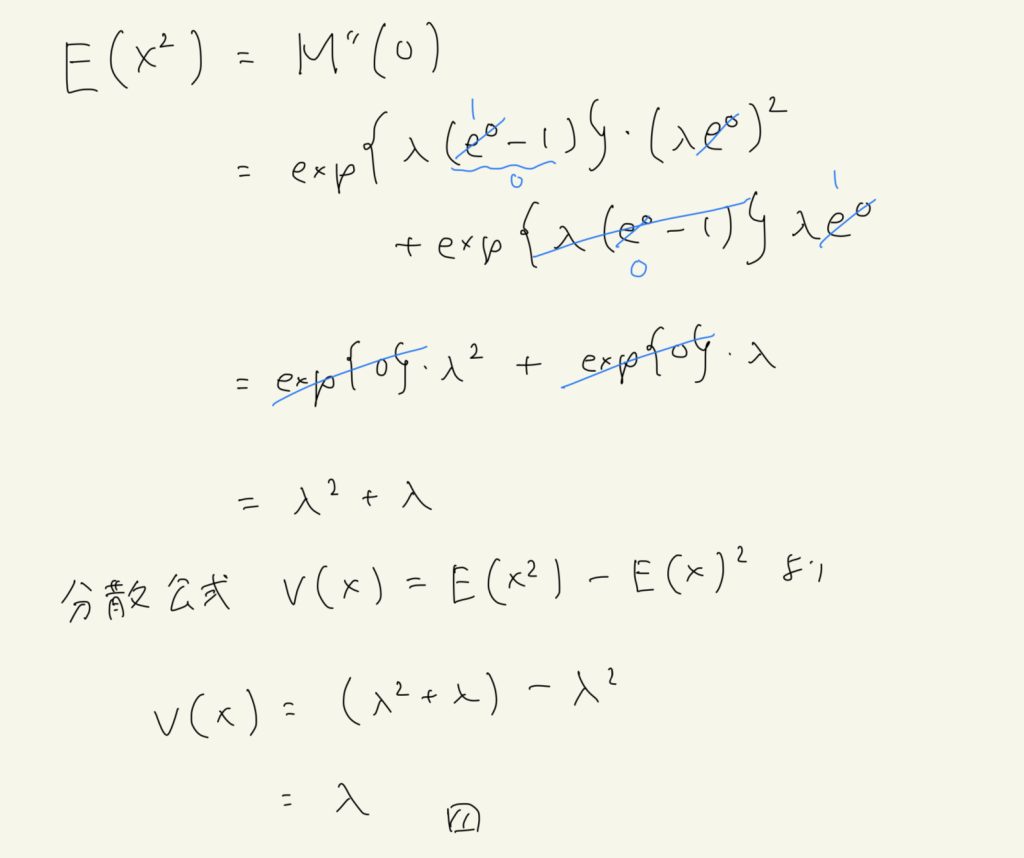
参考にした本
通称「赤本」と呼ばれている有名な良書。



コメント