二項分布は結果が2通り(例えば「成功」と「失敗」)の試行をn回行って、x回成功する(失敗でもいい)確率を表す分布である。
n回試行を行うが各回は独立であり成功確率がpならば、pは各回で変化してはならない。
確率分布は離散型で、\( x=0,1,\cdots,n \)に対して次のような式になる。
$$
f(x) = {}_n \mathrm{C}_k p^x (1-p)^{n-x}
$$
この式は成功がx回、失敗がn-x回起こる確率を、n回のうち、どの回で成功するかの組み合わせの数だけ考えた式になっている。
良く分からない方は、高校数学の「組合せ」を復習してほしい。
確率pで成功する試行をn回行った時、X回成功するとする。このとき、Xは確率変数であり、その分布は二項分布\( Bi(n, p) \)に従う。
確率変数Xが二項分布\( Bi(n, p) \)に従っている時、期待値、分散は次のようになる。
$$
E(X) = np
$$
$$
V(X) = np(1-p)
$$
この記事では、上の2式をモーメント母関数を使って証明する。
モーメント母関数は英語でmoment generating functionと言い、モーメントを生み出す関数という意味だ。日本語では「母」のところが、英語の「generating」に対応している。
また、モーメントとは\( E(X^r) \)のことであり。モーメント母関数は微分と変数に0を代入することで、全ての次数のモーメントを生成することができる。
モーメント母関数は次式で定義される。
$$
M(t) = E(e^{tX})
$$
モーメント母関数について詳細はここでは書かないが、証明のために次の2式が成り立っていることを前提にしたい。
$$
E(X) = M'(0)
$$
$$
E(X^2) = M^{\prime\prime}(0)
$$
これらの前提を元に二項分布\( Bi(n, p) \)の期待値、分散の式を手書きで証明する。

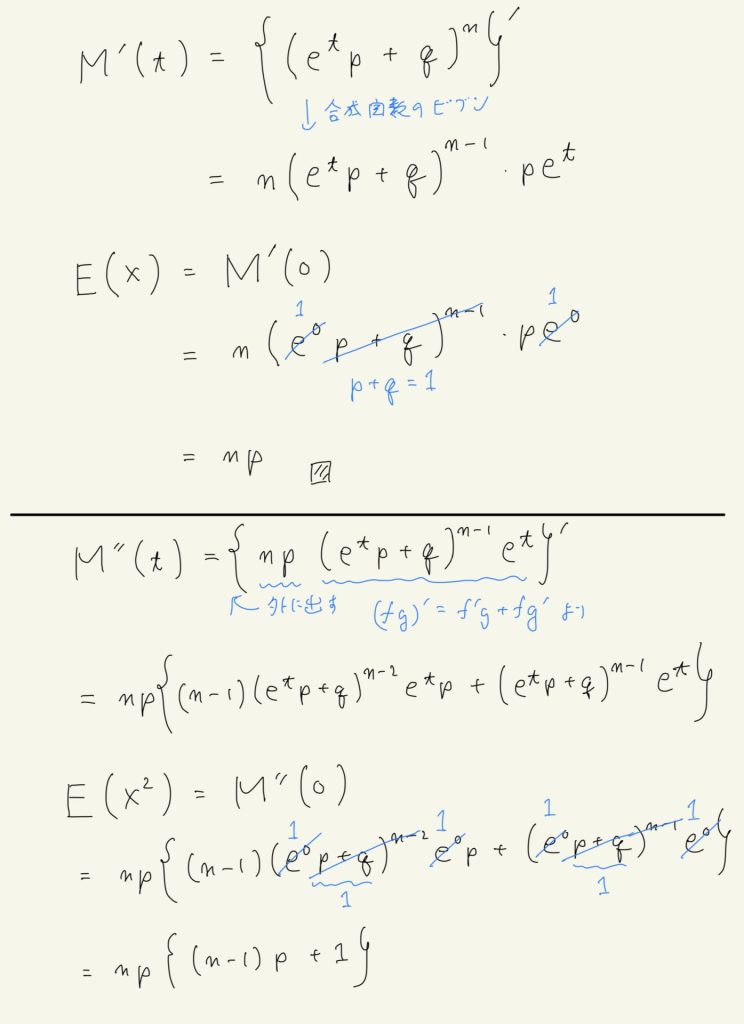
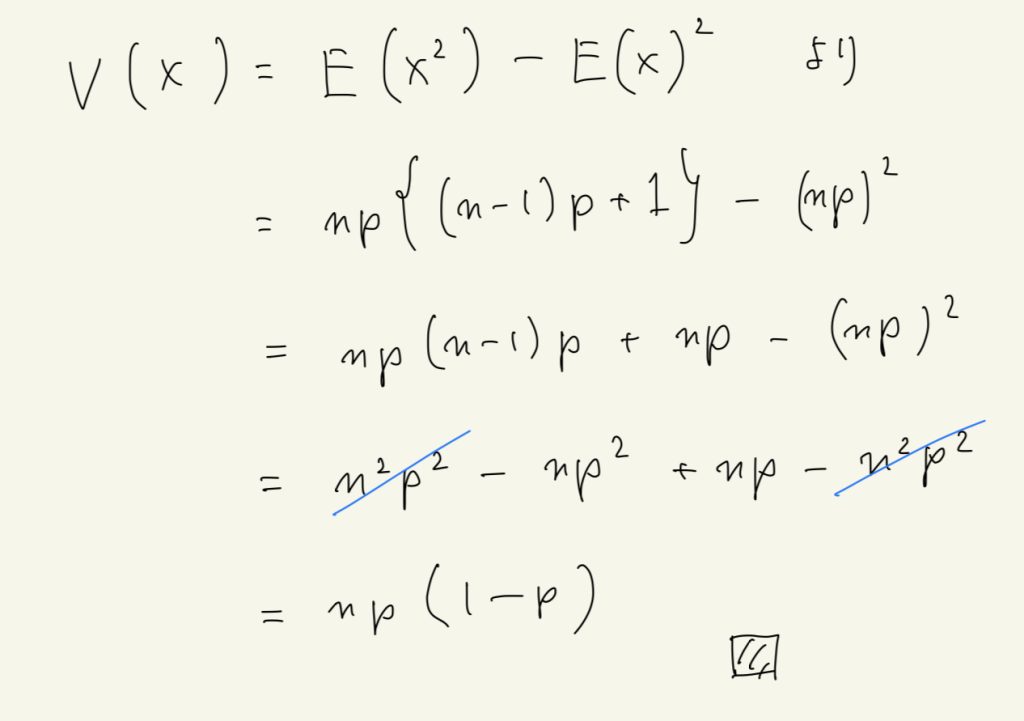



コメント