チェビシェフの不等式の解説
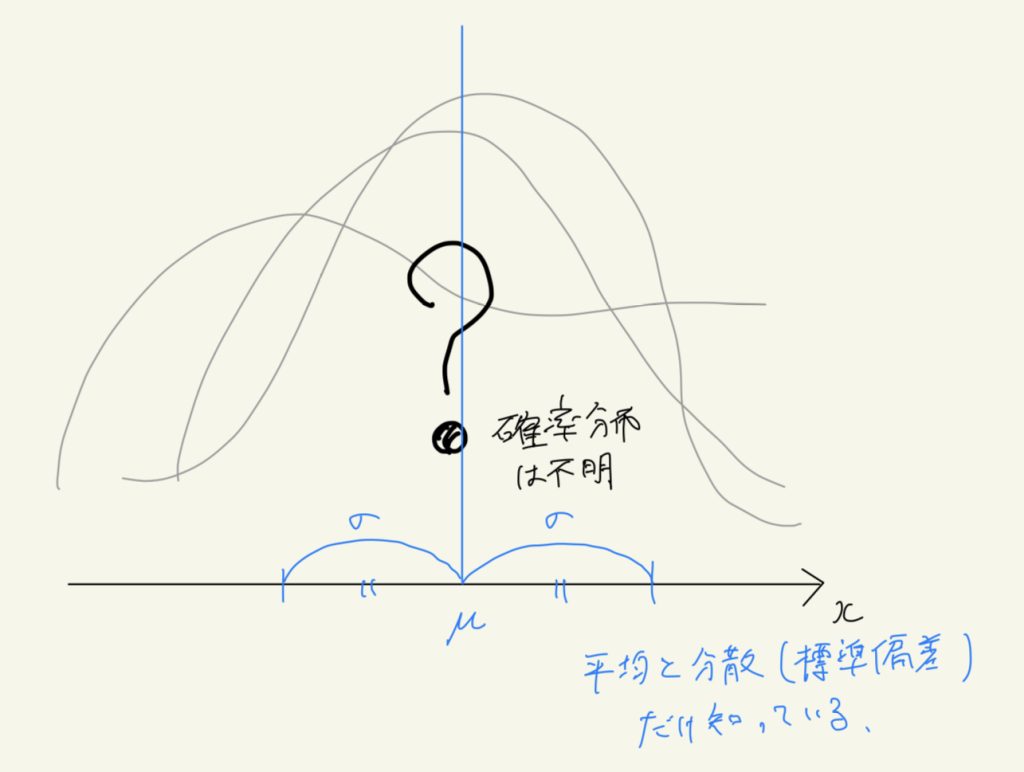
チェビシェフの不等式は、確率変数Xについて、確率分布(確率関数や確率密度関数)は分かっていないが、期待値\( \mu \)と分散\( \sigma^2 \)だけ知っている時、確率変数Xが期待値\( \mu \)から標準偏差\( \sigma \)の定数倍より離れた値を取る確率の上限を示した不等式である。
逆に言えば、確率変数Xが期待値\( \mu \)から標準偏差\( \sigma \)の定数倍以内の値を取る確率の下限を示す。
チェビシェフの不等式は確率分布を仮定していないため、大雑把な評価である。
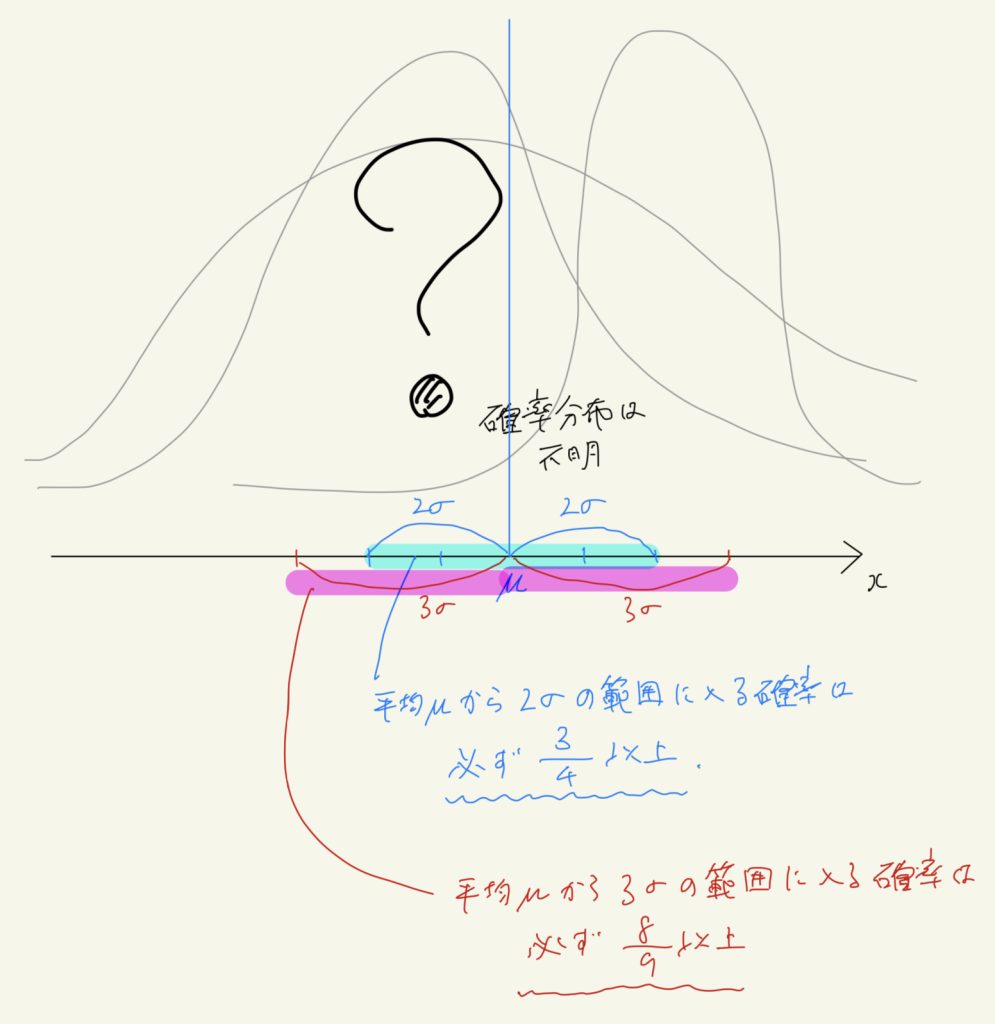
下の画像で示しているように、期待値\(\mu\)と標準偏差\(\sigma\)のみ分かっている時、平均\( \mu \)から\( 2\sigma \)の範囲に入る確率は必ず3/4以上というようなことがチェビシェフの不等式から言える。
チェビシェフの不等式の数式
チェビシェフの不等式は次のようになる。
$$
P(|X – \mu| \geq \lambda \sigma) \leq \frac{1}{\lambda^2}
$$
もしくは次のようにも表せる。
$$
P(|X – \mu| \lt \lambda \sigma) \geq 1 – \frac{1}{\lambda^2}
$$
チェビシェフの不等式の証明
以下の証明は「スッキリわかる確率統計」を参考にした。
Xが連続型の場合のみ証明する。Xの確率密度関数をf(x)とする。

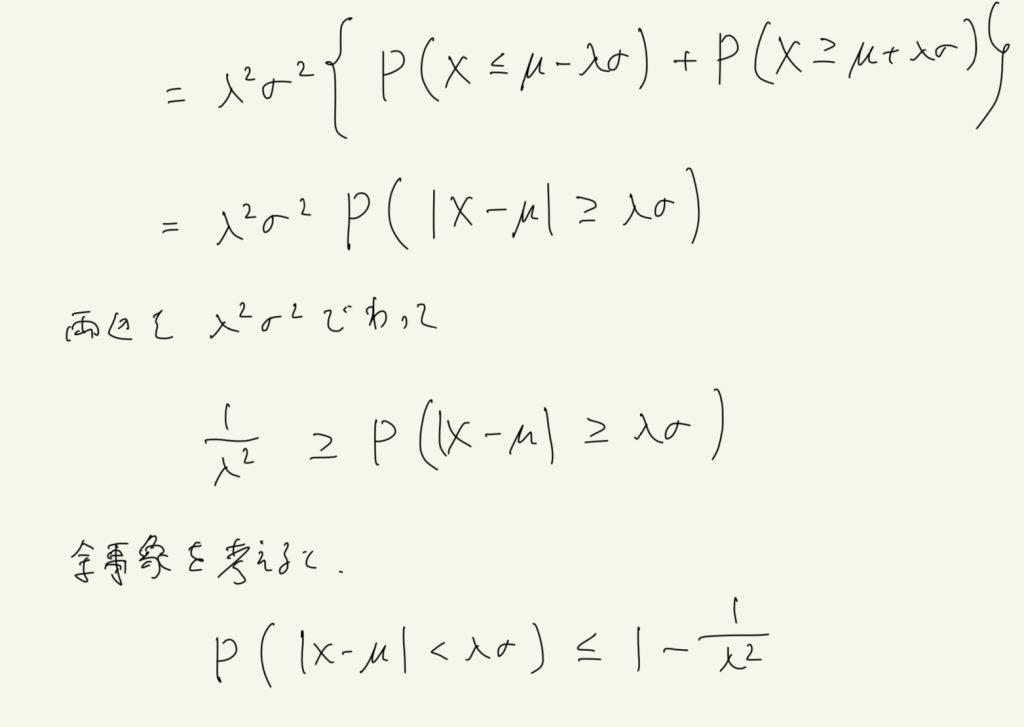




コメント