この記事の内容は「スッキリわかる確率統計: ―定理のくわしい証明つき―」という本を参考にして書かれています。正規分布のモーメント母関数の導出など、「統計学入門(赤本)」には書かれていない内容も、この本には書いてあることが多々あるので個人的にオススメです。
カイ2乗分布のモーメント母関数の導出
前提知識として次のガンマ関数\( \Gamma(s) \)の定義を使います。
\( s>0 \)のとき
$$
\Gamma(s) = \int_0^{\infty} e^{-x} x^{s-1} dx
$$
カイ2乗分布の確率密度関数からモーメント母関数を導出します。
自由度nのカイ2乗分布の確率密度関数は次のようになります。
$$
\begin{eqnarray}
f(x)
=
\begin{cases}
\frac{1}{2^{\frac{n}{2}} \Gamma ( \frac{n}{2} )} x^{\frac{n}{2} – 1} e^{-\frac{x}{2}} & (x \geq 0) \\
0 & (x \lt 0)
\end{cases}
\end{eqnarray}
$$
以下、手書きで導出します。
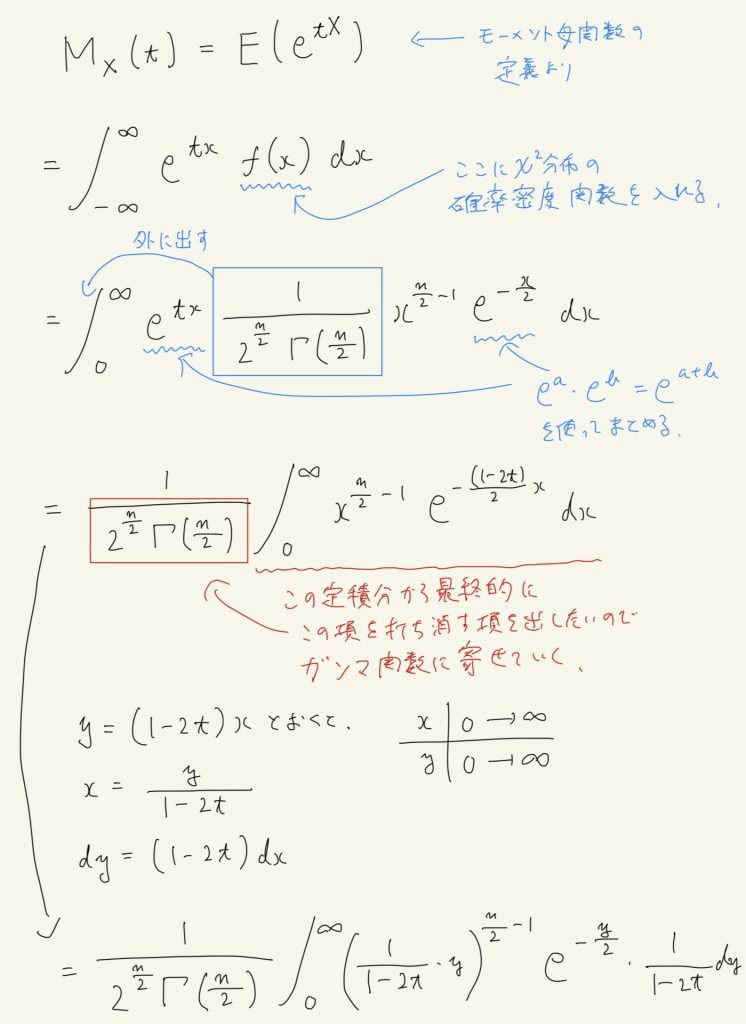




コメント