確率分布の解説（直感的な説明）

確率分布を理解するためには、先に確率変数を理解する必要がある。
確率変数については下の記事で解説したので参照して欲しい。

確率変数・実現値の直感的な説明

確率変数と実現値についての厳密でない直感的な説明をしました。

mathnyumon.com

2023.05.22

確率変数には「離散型の確率変数」と「連続型の確率変数」があるが、離散型の確率変数に対して離散型の確率分布が、連続型の確率変数に対して連続型の確率分布がそれぞれ対応する。

「離散型の確率分布」と「連続型の確率分布」は基本となる考え方は同じだが、扱いが多少異なるので、この記事ではまず「離散型の確率分布」について解説する。

上の確率変数の記事と同じ例で考える。

1等(100万円)、2等(1万円)、3等(100円)、4等(はずれ、0円)の宝くじを考える。

ここで、何等が出るかを確率変数Xとすると、確率変数Xの取りうる値（これを実現値という）は1 or 2 or 3 or 4だ。

確率変数の実現値と、その実現値を取る確率を全て表したもの、それが確率分布だ。

この確率分布という用語はいくつかのものを表しており、例えば以下のような表も、確率変数の実現値と、その実現値を取る確率を全て表しているので、確率分布だ。

下のグラフも同様に、確率変数の実現値と、その実現値を取る確率を全て表しているので、確率分布だ。

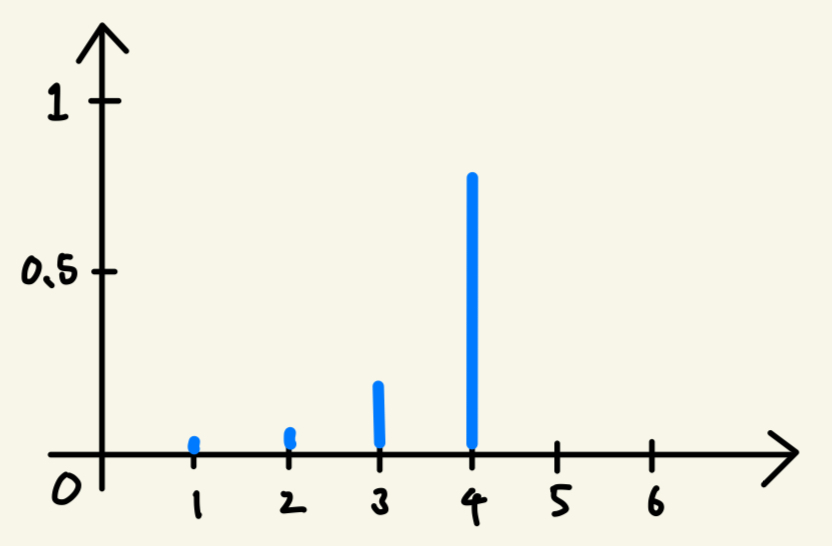
また、以下のような関数も同様に確率分布だ。

$$
\begin{eqnarray}
f(x)
=
\begin{cases}
\frac{1}{100} & (x=1) \\
\frac{3}{100} & (x=2) \\
\frac{20}{100} & (x=3) \\
\frac{76}{100} & (x=4) \\
0 & (それ以外のx)
\end{cases}
\end{eqnarray}
$$

確率分布の直感的な説明

以上のようなものが確率分布だが、直感的な説明をしよう。

全ての実現値にわたって確率を合計した時、合計が1になることは分かると思う。

ここで逆に考えて、合計が1になる確率をそれぞれの実現値にどのように割り振った（分布させた）かが、確率分布だ。

どのように確率を割り振った（分布させた）かが分かるものは確率分布と言えるので、上記のように表や、グラフ、関数も確率分布と呼べる。