【統計検定2級】共分散の性質（計算法則）と証明

この記事では、統計検定2級の問題を解くのに必要だが、一般的な統計の本にはあまり載っていない共分散の性質について列挙＆証明する。

共分散の性質

$$
V(X+Y) = V(X) + V(Y) + 2Cov(X, Y) \tag{a}
$$

$$
V(X+Y+Z) = V(X) + V(Y) + V(Z) + 2Cov(X,Y) + 2Cov(X,Z) + 2Cov(Y,Z) \tag{b}
$$

$$
Cov(X+a,Y) = Cov(X,Y) \tag{c}
$$

$$
Cov(aX,Y) = aCov(X,Y) \tag{d}
$$

$$
Cov(X,Y+Z) = Cov(X,Y) + Cov(X,Z) \tag{e}
$$

$$
Cov(X,Y+Z+W) = Cov(X,Y) + Cov(X,Z) + Cov(X,W) \tag{f}
$$

証明の前に共分散の定義

$$
Cov(X, Y) = E[(X-E[X])(Y-E[Y])]
$$

共分散の性質の証明

$$
V(X+Y) = V(X) + V(Y) + 2Cov(X, Y) \tag{a}
$$

の証明

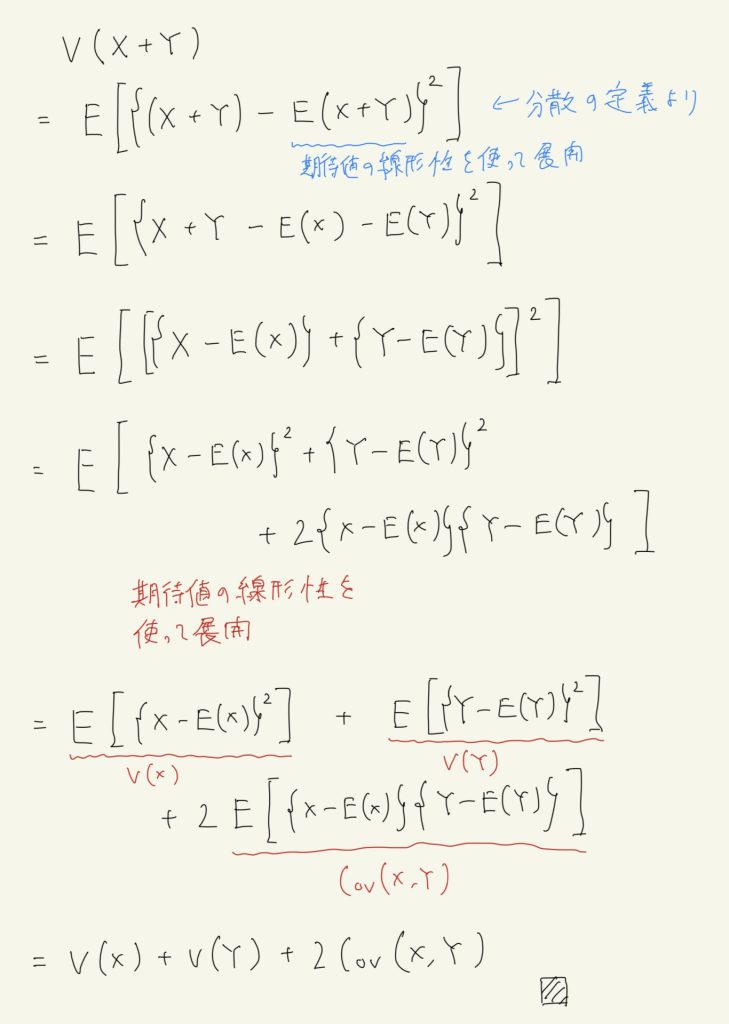
$$
V(X+Y+Z) = V(X) + V(Y) + V(Z) + 2Cov(X,Y) + 2Cov(X,Z) + 2Cov(Y,Z) \tag{b}
$$

の証明

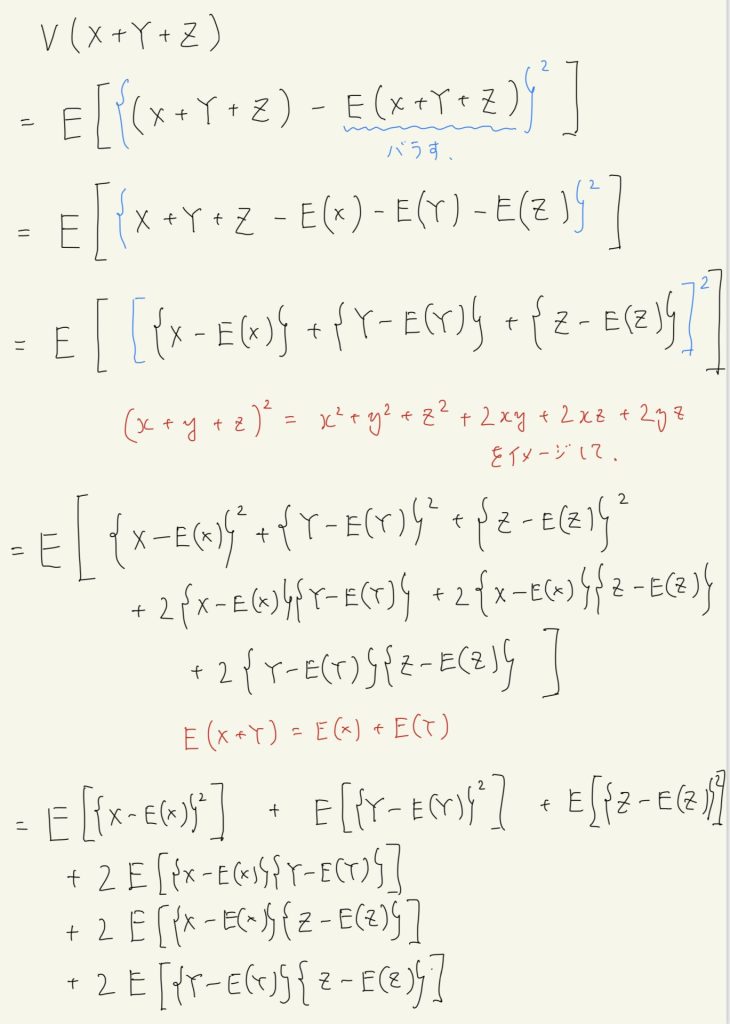
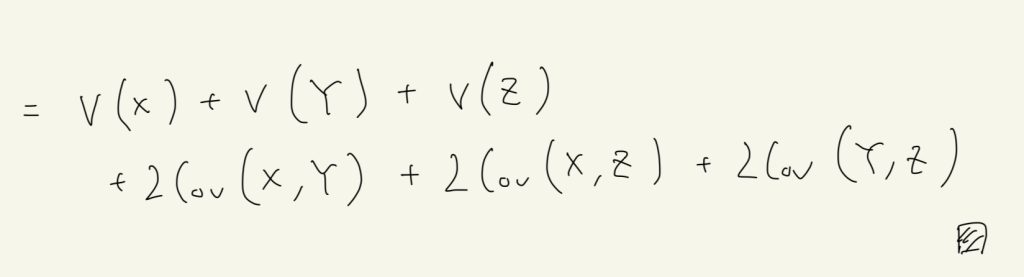
$$
Cov(X+a,Y) = Cov(X,Y) \tag{c}
$$

の証明

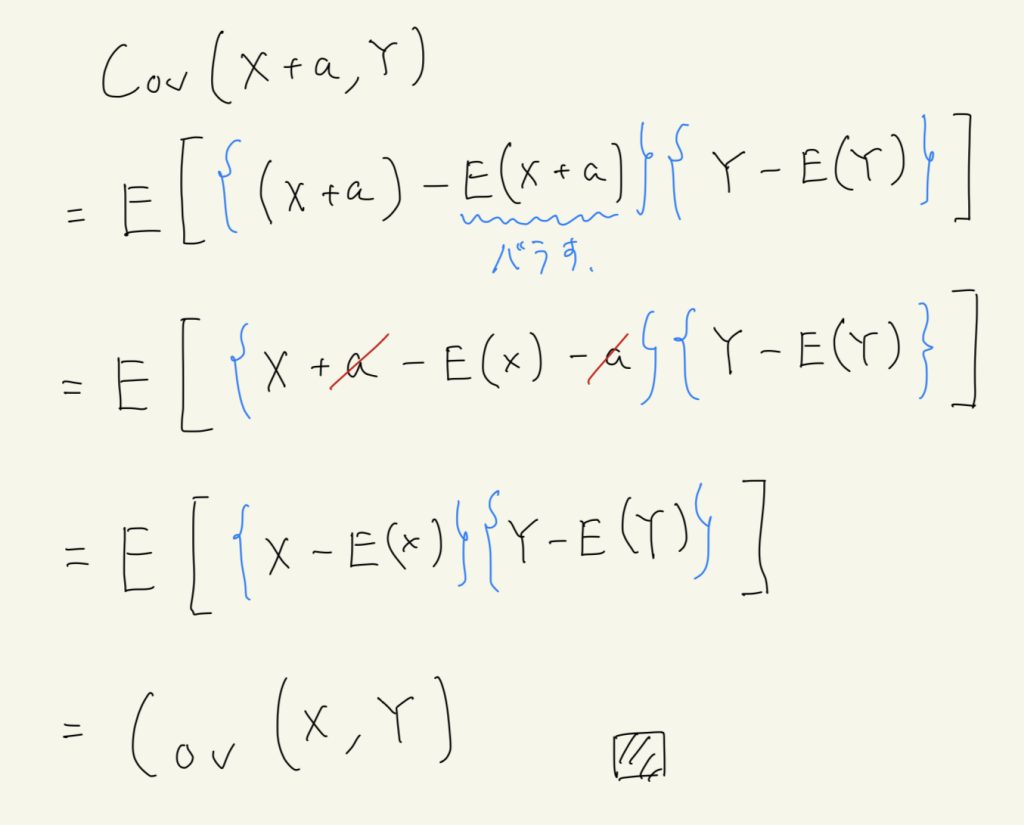
$$
Cov(aX,Y) = aCov(X,Y) \tag{d}
$$

の証明

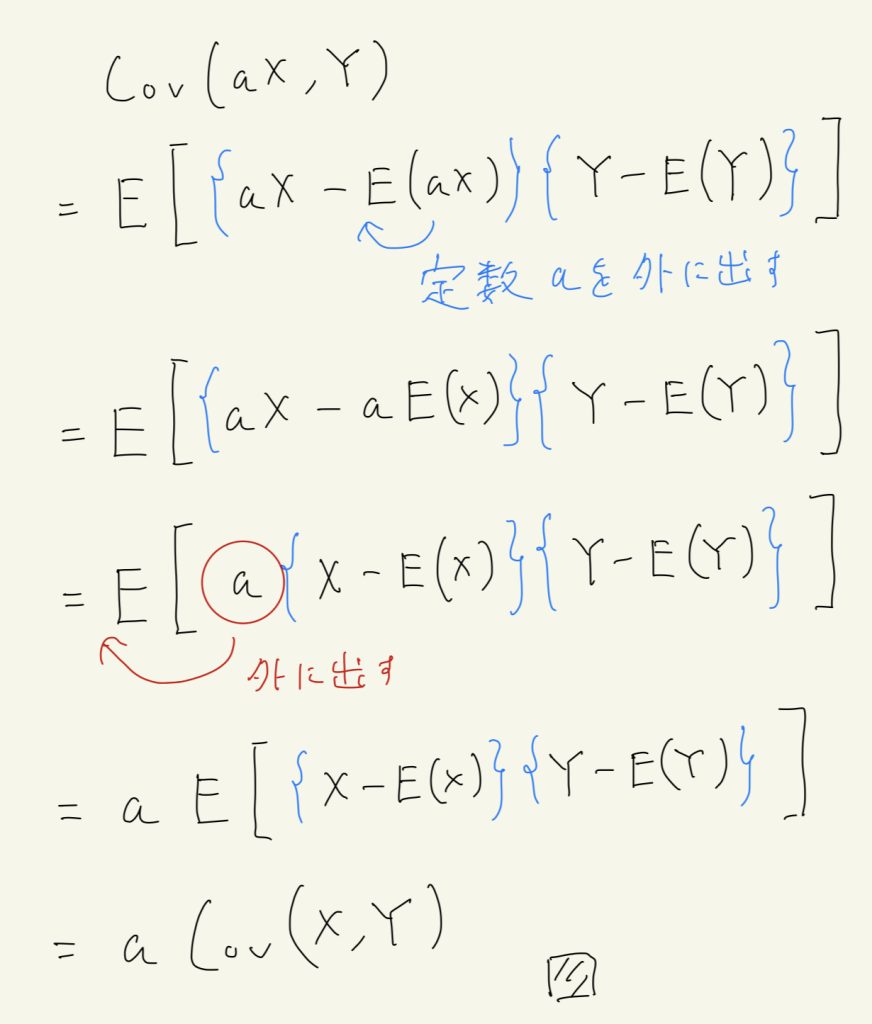
$$
Cov(X,Y+Z) = Cov(X,Y) + Cov(X,Z) \tag{e}
$$

の証明

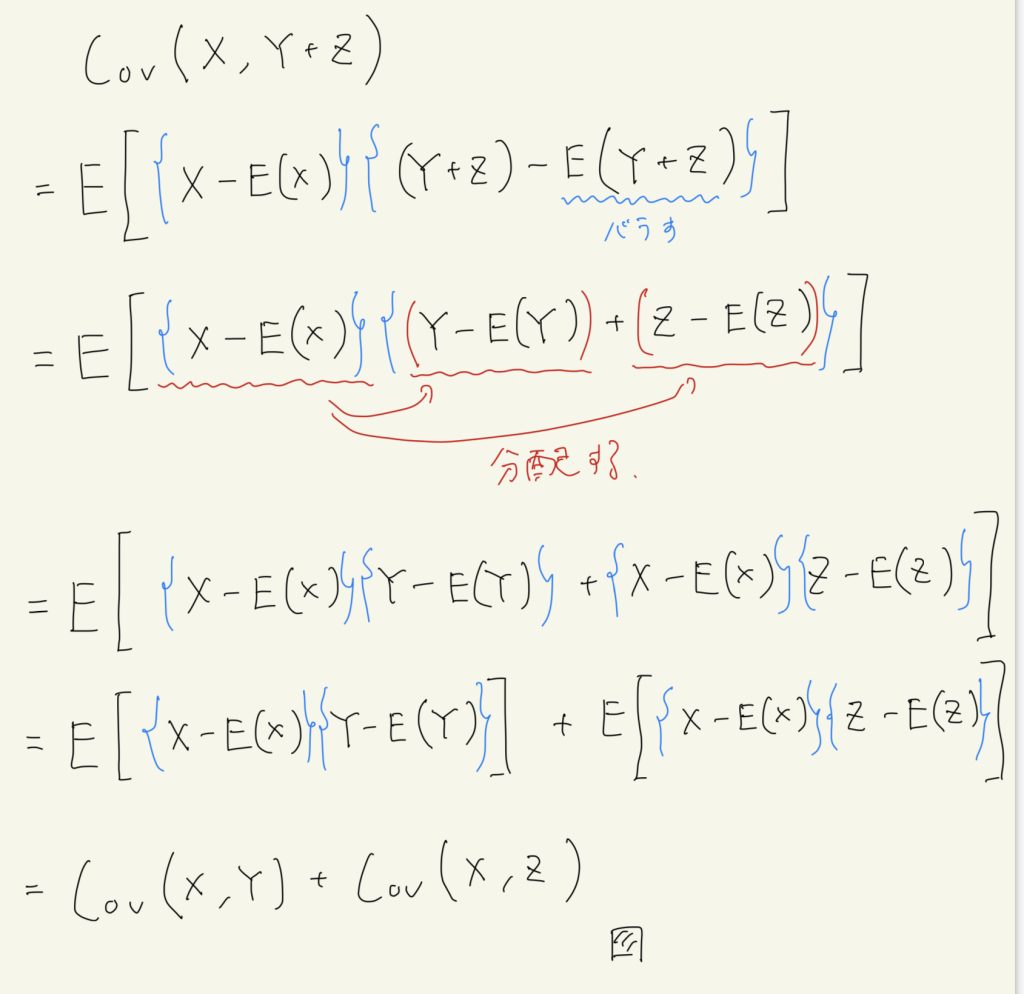
$$
Cov(X,Y+Z+W) = Cov(X,Y) + Cov(X,Z) + Cov(X,W) \tag{f}
$$

(f)は(e)の証明を少し修正すれば示せる。