仮説検定のふわふわ解説

内容量100gと書いてあるお気に入りのアイスクリームがあるとします。

毎日食べているのですが、最近食べごたえを感じなくなってきました。気になったので本当に100g入っているか10個正確に重さを測ってみることにしました。

その結果が以下。

アイス	A	B	C	D	E	F	G	H	I	J
重さ(g)	98	95	101	102	93	97	94	95	99	100

総和は974gで1個平均は97.4gです。
分散は8.64で標準偏差は2.94gです。

製品表示には100gと書いてあるのに、調べてみたら平均は97.4gと100gより小さい。
けれど、個別に見ると100gを超えているアイスもある。

あなたは考えました。アイスの製造会社がステルス値上げをしていて、表示より少ない内容量のアイスを製造していると。

ここで仮説検定の出番です。

アイスの製造会社が製造している本当の内容量を$ \mu $とします。

あなたの仮説$ H_1 $は、この$ \mu $が100gより小さいということ、つまり

$$
H_1 : \mu < 100
$$

です。この$H_1$を対立仮説と言います。
仮説検定をするために帰無仮説$H_0$というものを用意します。

$H_0$は無に帰する仮説なので、この場合、アイスの製造会社が100gのアイスを製造していることです。つまり

$$
H_0 : \mu = 100
$$

仮説検定の手順は

今回の例で、次を仮定します。

まず、アイスクリームの重さは正規分布に従っているとする。
また、その正規分布の分散だけ分かっているとして、その分散を9とする。

仮説検定を進めます。

まず帰無仮説$H_0$を仮定し、アイスクリームの重さは正規分布$ N(100, 9) $に従っているとします。

このとき、調べた10個のアイスの重さの平均、つまり標本平均$ \bar{X} $は正規分布$ N(100, \frac{9}{10}) $に従います。

標本平均$ \bar{X} $の実現値は97.4gなので、この実現値（およびそれより外れた値）が正規分布$ N(100, \frac{9}{10}) $から得られる確率を考えます。

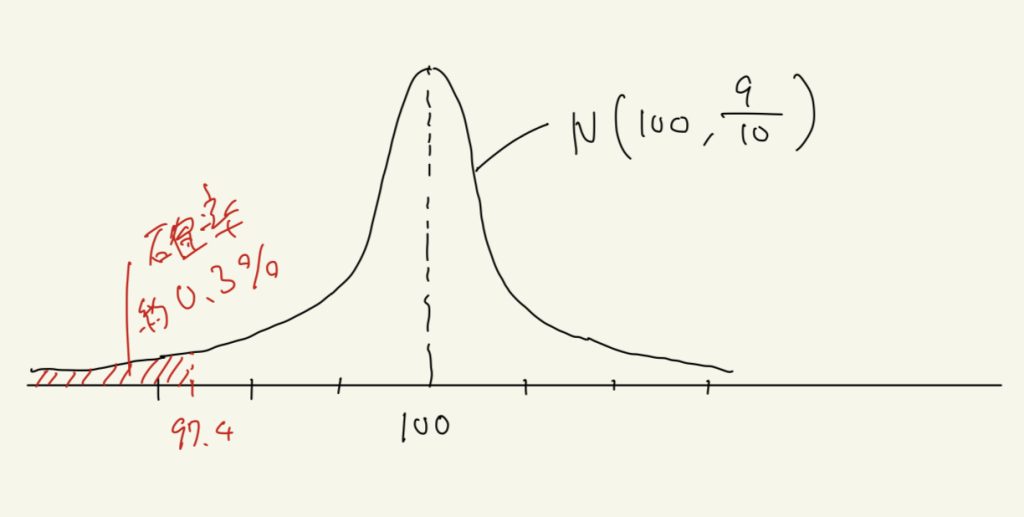
計算したところ、その確率は約0.3%という事がわかりました。

0.3%の確率で起こる現象が起こったと考えるよりも、仮定した帰無仮説$H_0$が間違っていたと考えるほうが妥当なので、帰無仮説$H_0$を棄却し、対立仮説$H_1$を採択します。

つまり、あなたの考え通り、製造会社がステルス値下げをしていて内容量を偽っているということです。

後日談：お気に入りのアイスは、カップの底までびっしりアイスが詰まっていて好きだったのですが、最近見直したら上げ底に変わっていました。ショック！！

半分、自分の体験で書きました。

参考にした本

通称「赤本」と呼ばれている有名な良書。