この記事では下の公式を解説します。
$$
\int_a^b \int_c^d f(x)g(y)dxdy = \left( \int_c^d f(x) dx \right) \left( \int_a^b g(y) dy \right)
$$
この公式は、被積分関数がxの関数とyの関数の積で表され、xに関しても、yに関しても積分区間が定数の時に成り立つ公式です。
この公式は、色々な場面でしれっと使われる割に説明されることもなく、全く説明がない参考書も多くあります。「1冊でマスター 大学の微分積分」という本には、この公式が載っていますが、簡単な解説に留まっています。分からない方がいるかもしれないので、解説します。
以下、手書きで解説します。




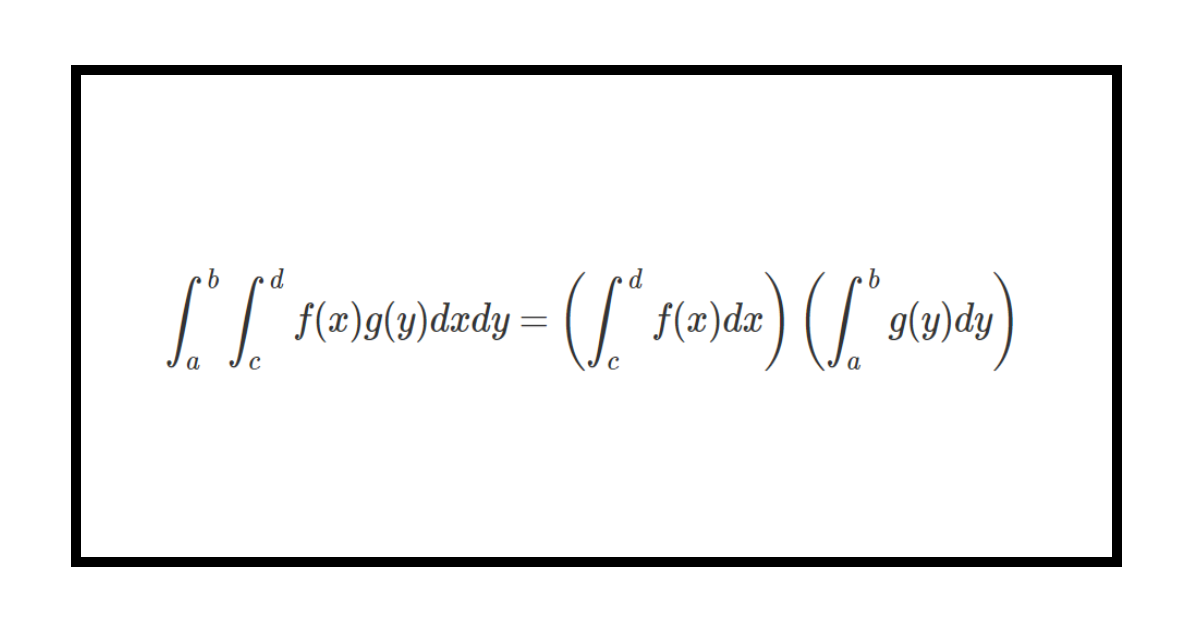

コメント