※記事の内容に間違い等あればコメントで教えてください。
ベータ関数の定義
ベータ関数は次のように定義される。
\( p>0, q>0 \)の時
$$
B(p, q) = \int_0^1 x^{p-1} (1-x)^{q-1} dx
$$
重要な性質と証明
ベータ関数の重要な性質は、次のようなガンマ関数との関係性を表す式である。
$$
B(p, q) = \frac{\Gamma(p) \Gamma(q)}{\Gamma(p + q)} \tag{a}
$$
ガンマ関数の定義式は下のようになっている。
$$
\Gamma(s) = \int_0^{\infty} e^{-x} x^{s-1} dx
$$
以下、式(a)の証明を行っていく。「スッキリわかる確率統計: ―定理のくわしい証明つき―」という本の証明を参考にした。





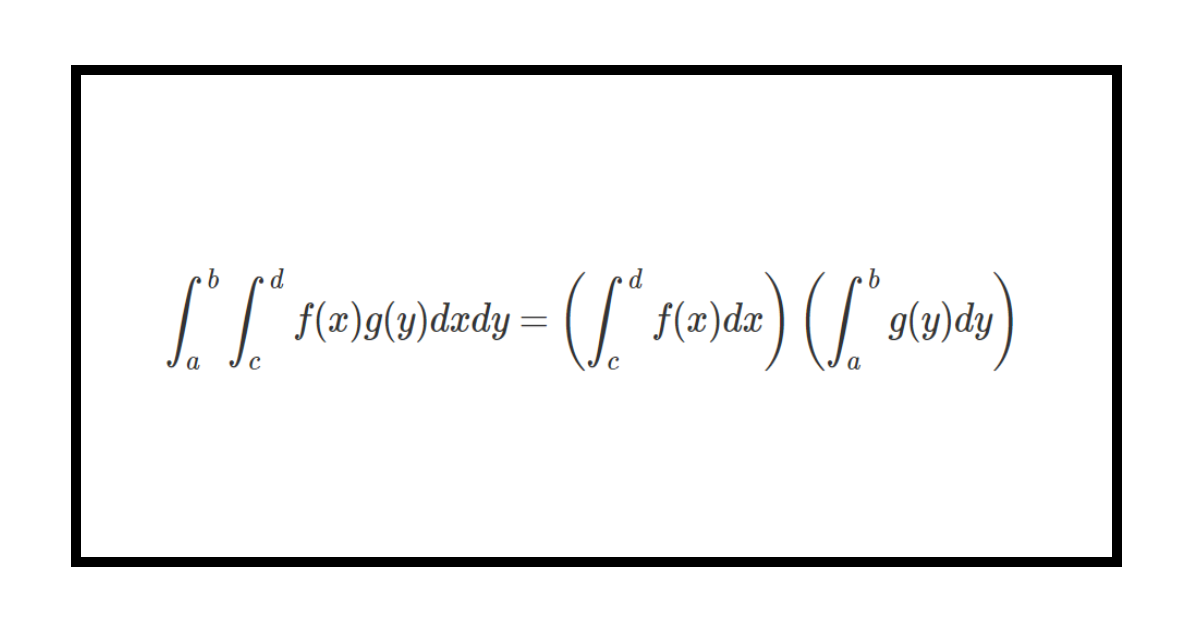
コメント