前提
不偏分散(標本分散とも呼ばれる)は次の式で表される。
$$
s^2 = \frac{1}{n-1}\{(X_1-\bar{X})^2 + \cdots + (X_n-\bar{X})^2\}
$$
ここで標本\( X_1, \cdots, X_n \)は母集団分布(母平均\( \mu \)、母分散\( \sigma^2 \))に従う独立な確率変数である。
また標本平均\( \bar{X} \)は次のように定義される。
$$
\bar{X} = \frac{X_1 + \cdots + X_n}{n}
$$
標本平均\( \bar{X} \)について、次の式が成り立っている。
$$
E(\bar{X}) = \mu \\
V(\bar{X}) = \frac{\sigma^2}{n}
$$
ここまでを前提として、統計量\( s^2 \)が不偏性を持っていることを証明する。
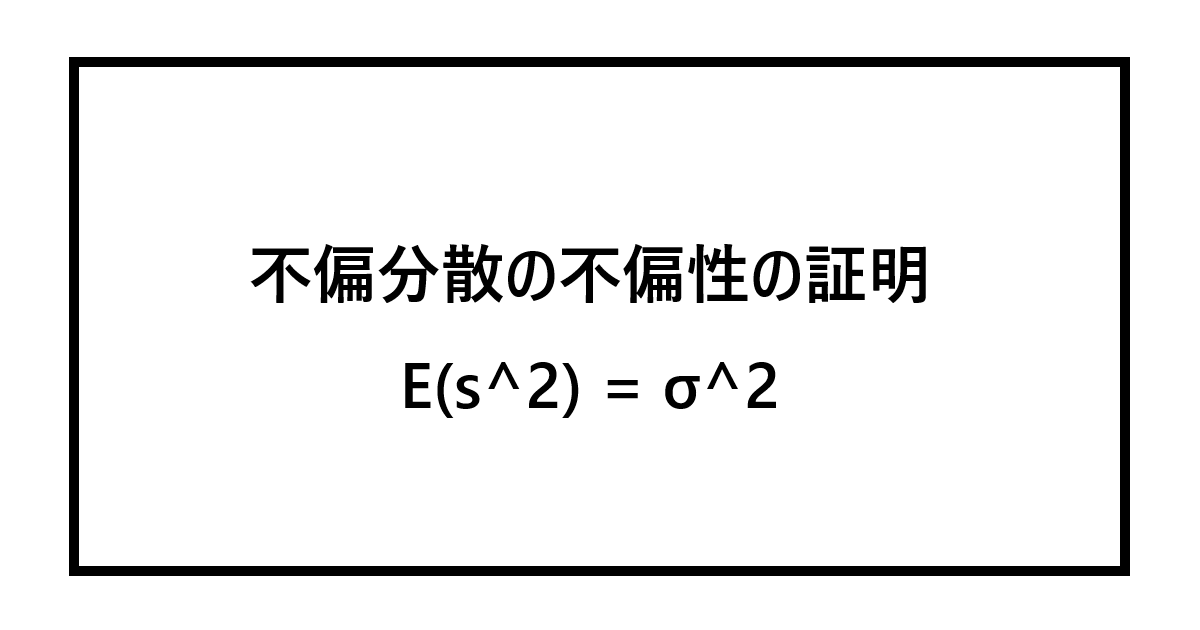
不偏性とは、統計量が持つべき性質の1つで、統計量の期待値を取った時に、母数(母平均や母分散など)に一致する性質である。この不偏性を数式で表現すると次のようになる(母分散の場合)。
$$
E(s^2) = \sigma^2 \tag{a}
$$
(豆知識:統計の本で\( \mu \)や\( \sigma \)などのギリシャ文字で書かれる定数は母集団のパラメータであることが多い)
証明
以下、手書きで式(a)を証明する。

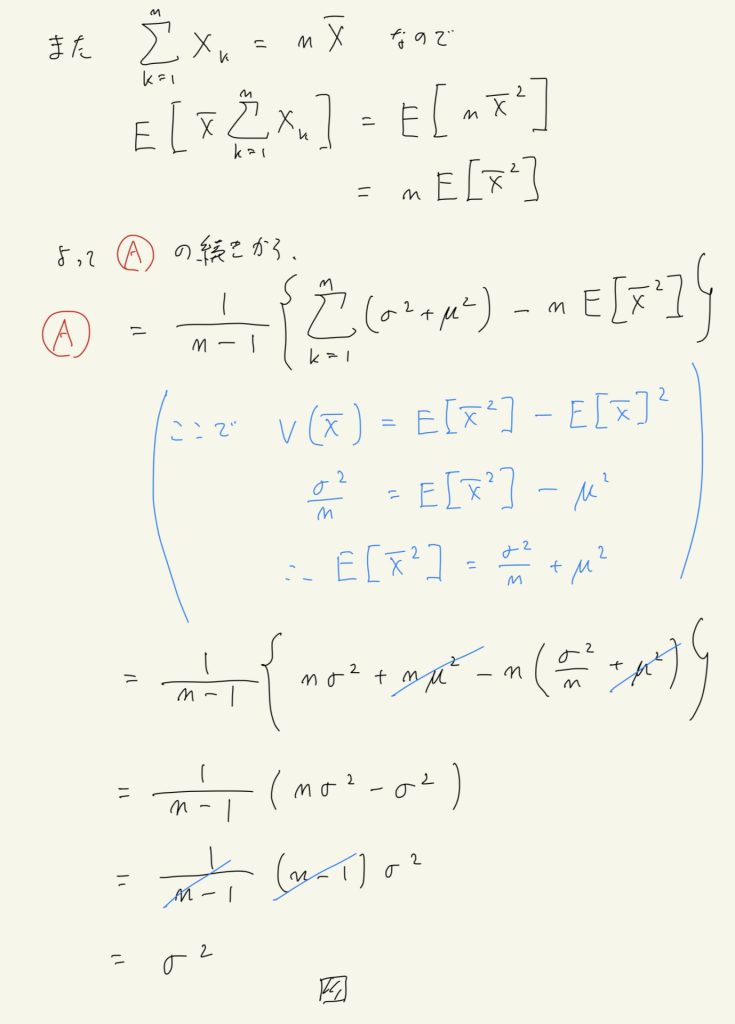
参考にした本
通称「赤本」と呼ばれている有名な良書。





コメント