何か間違いなどありましたら、コメントで教えてください。
期待値の演算Eについての重要な性質
XとYを確率変数、cを単なる定数とする。
$$
E(c) = c \tag{a}
$$
$$
E(X + c) = E(X) + c \tag{b}
$$
$$
E(cX) = cE(X) \tag{c}
$$
$$
E(X + Y) = E(X) + E(Y) \tag{d}
$$
順番に解説する。
まず(a)は定数の期待値は、その定数自身ということだ。
定数は確率変数ではないので、期待値はその定数自身ということだ。
(※ここでは簡単に性質を説明するが、後で定義式を用いて証明する)
(b)、(c)は期待値の演算について、定数は簡単に外に出せるということを表している。
定数について、素直な式変形が可能だと理解してほしい。
これについても証明は後述する。
(d)は2つの確率変数が関わる少し特殊なものだ。
この性質は「期待値の加法性」と呼ばれている。
これについて少し注意して欲しいのは、確率変数Xと確率変数Yが独立でも独立でなくとも、この性質は成立するということだ。
今後、複数の確率変数が関わる性質を表す公式が出てきた時、それらの確率変数が独立の場合と、独立でない場合で直感的な式変形ができなくなる場合があるので、少し気に留めておいてほしい。
証明のために必要な定義 1
確率変数Xの関数\( \phi (X) \)についての期待値の定義は、
離散型確率変数Xの場合
$$
E(\phi (X)) = \displaystyle \sum_x \phi (x) f(x)
$$
連続型確率変数Xの場合
$$
E(\phi (X)) = \displaystyle \int_{-\infty}^{\infty} \phi (x) f(x) dx
$$
証明のために必要な定義 2
確率変数XとYについての期待値の定義は、
XとYが離散型確率変数の場合
$$
E(\phi (X, Y)) = \displaystyle \sum_x \sum_y \phi (x, y) f(x, y)
$$
XとYが連続型確率変数の場合
$$
E(\phi (X, Y)) = \displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \phi (x, y) f(x, y) dx dy
$$
証明
以降、手書きになるが、証明を載せておく。
(字が汚くてすみません・・・。次からはなるべく丁寧に書きます。)
(a)の証明

(b)の証明
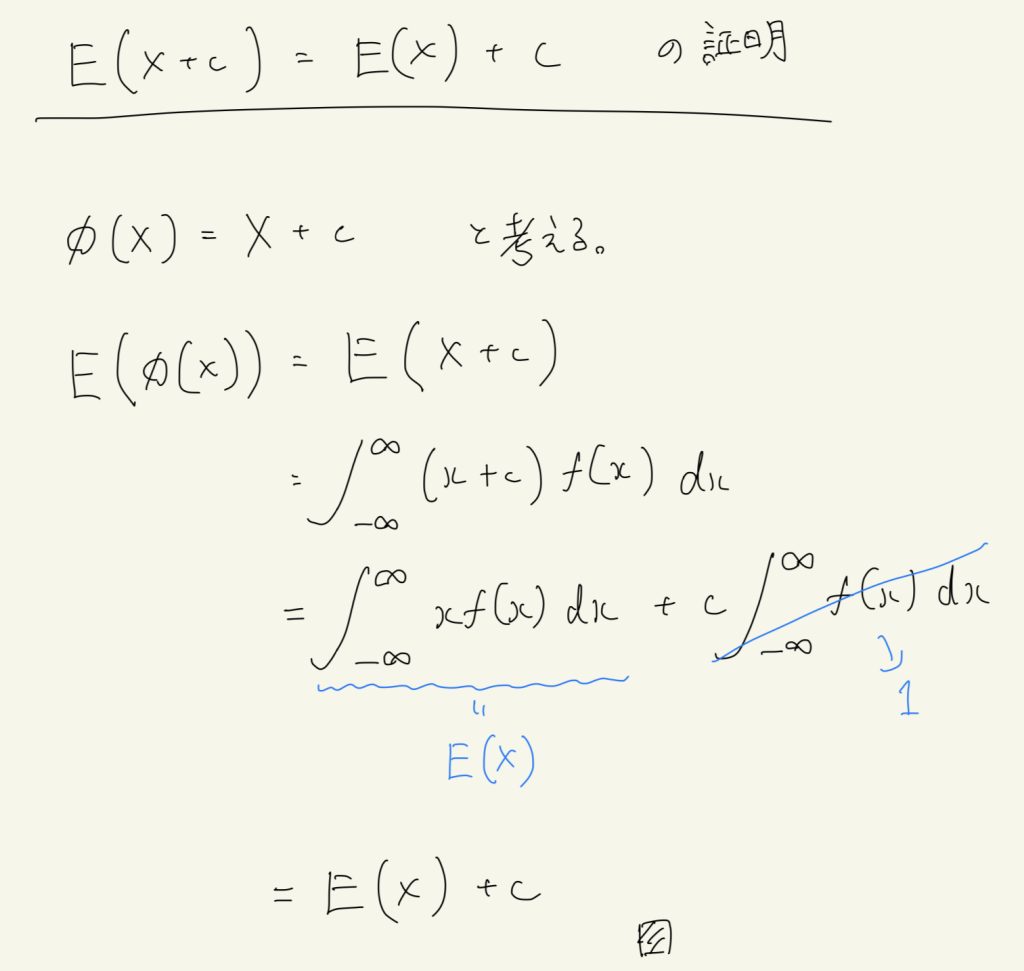
(c)の証明
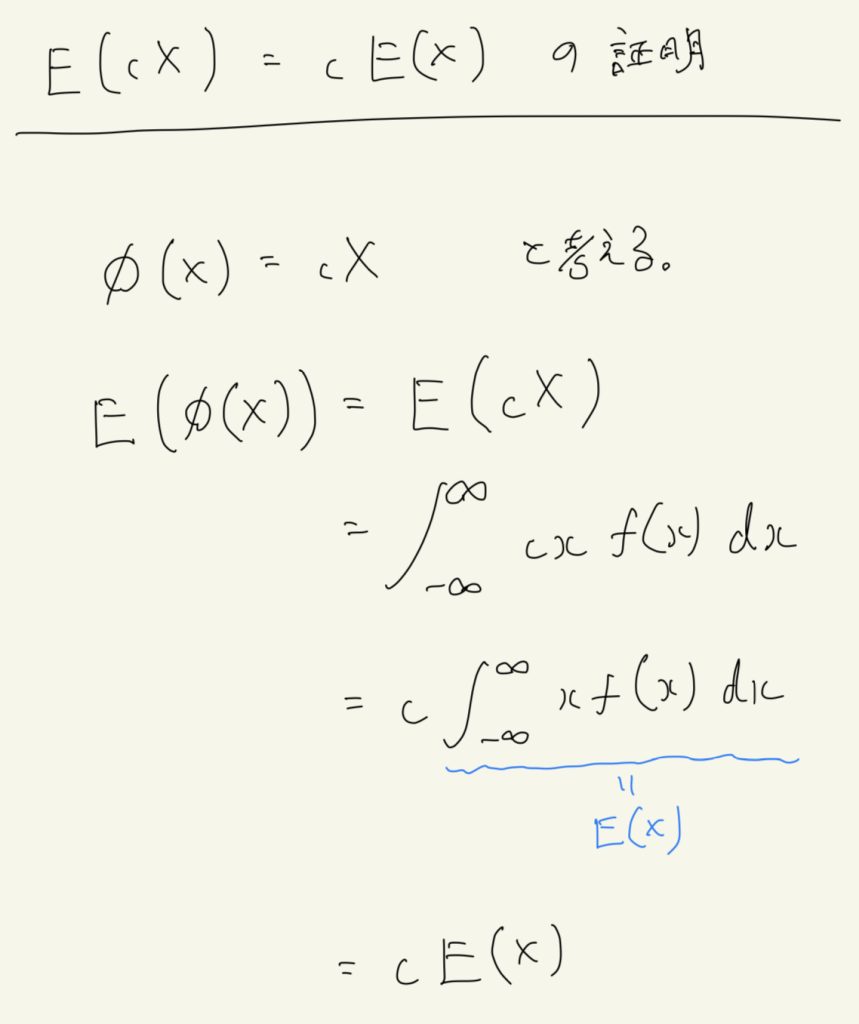
(d)の証明
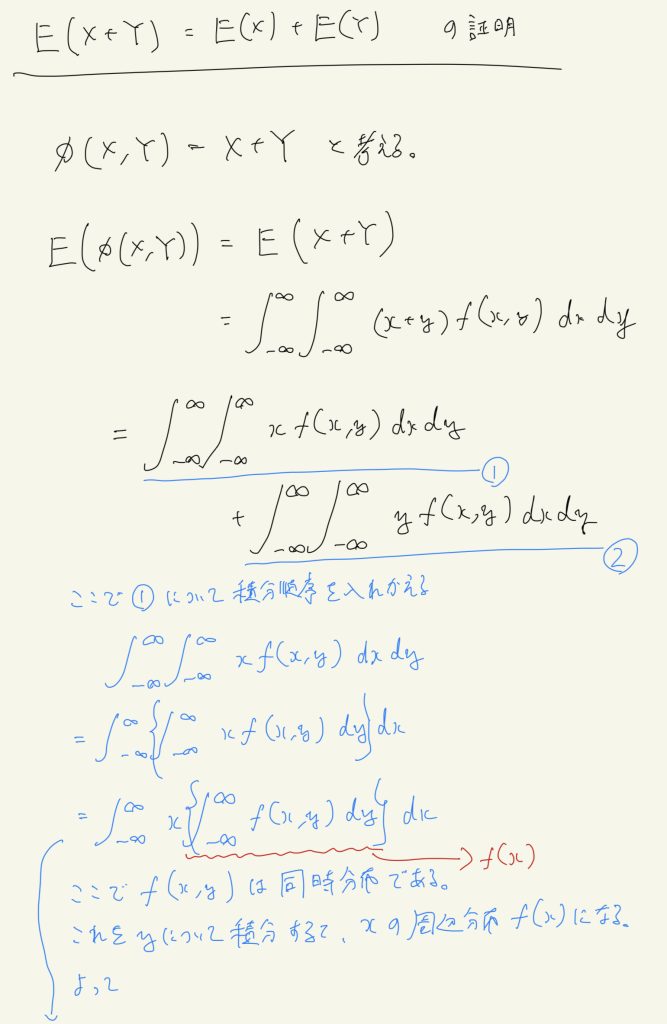

参考にした本
通称「赤本」と呼ばれている有名な良書。





コメント