正規分布の確率密度関数とその覚え方のコツ

正規分布$ N(\mu, \sigma^2) $の確率密度関数は次のようになります。

$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp \left({-\frac{(x-\mu)^2}{2\sigma^2}} \right)
$$

標準正規分布$ N(0, 1) $の確率密度関数は、上の式で$ \mu=0, \sigma=1 $を代入して

$$
f(x) = \frac{1}{\sqrt{2\pi}}\exp \left( – \frac{x^2}{2} \right)
$$

覚え方のコツ

この記事では正規分布$ N(\mu, \sigma^2) $の確率密度関数の覚え方について解説します。

統計検定（2級・準1級）で正規分布の確率密度関数を覚えている必要はあまり無いかもしれませんが、正規分布の確率密度関数を自然に覚えるくらい勉強しないと受からない気がします。（特に準1級）

この記事では覚え方のコツを紹介します。

正規分布に限らず確率密度関数は、本質的な本体の部分と、確率密度関数を定義域全体（正規分布の場合、－∞～∞）で積分した時に1にするための正規化定数に分けられます。

正規分布の確率密度関数の場合、確率密度関数の本質的な本体の部分は

$$
\exp \left ( – \frac{(x – \mu)^2}{2 \sigma^2} \right )
$$

であり、頭にくっついている

$$
\frac{1}{\sqrt{2\pi}\sigma}
$$

は、確率密度関数を下のように定義域全体で積分した時に1になるように、調整のため付けられている正規化定数です。

$$
\int_{-\infty}^{\infty} \left \{ \frac{1}{\sqrt{2\pi}\sigma}\exp \left({-\frac{(x-\mu)^2}{2\sigma^2}} \right) \right \} dx = 1
$$

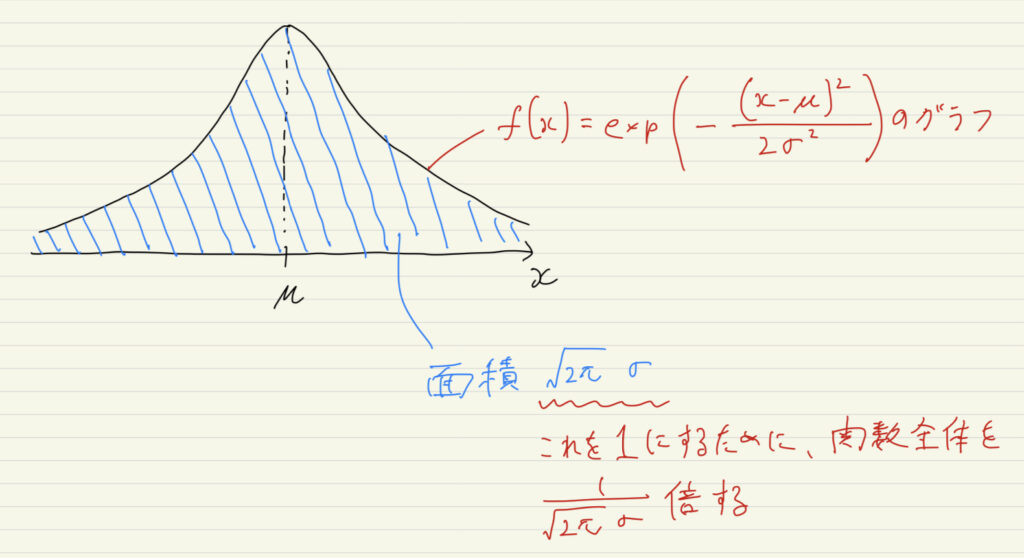
本体部分の積分を毎回するのは面倒なので、正規化定数は覚えてしまいましょう。

$ x=\mu $を中心とした左右対称のグラフを作りたいので、$ (x-\mu)^2 $という形を考えます。

$ (x-\mu)^2 $は$ x=\mu $を中心として、$ \mu $から左右同じ距離離れた点では同じ値を取ります。

$ \exp \left ( – (x-\mu)^2 \right) $の形を考えます。
この指数関数はxが$ \mu $から離れると、速く0に向かって小さくなります。
正規分布は平均$ \mu $から離れた値を取る確率密度は急速に小さくなることを表すために、指数関数が使われています。

分母の2は、確率密度関数を微分した時に$ (x-\mu)^2 $の部分から降りてくる2を相殺するために、簡単のために付けられたものだと思います。

最後に$ \sigma^2 $ですが、以下のように式を変形すると

$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left ( – \frac{1}{2} \left(\frac{x-\mu}{\sigma} \right)^2 \right )
$$

$ \left(\frac{x-\mu}{\sigma} \right)^2 $の部分は、標準化したような値の2乗になっており、標準化したい気持ちを汲み取ると$ \sigma $の2乗が当たり前に感じます。