期待値の演算については、下の記事で紹介しているように分かりやすい性質がいくつかあるが、2つの確率変数X、Yの積の期待値E(XY)については少し注意が必要なので紹介する。
確率変数XとYが独立ならば次の式が成り立つ。
$$
E(XY) = E(X)E(Y) \tag{a}
$$
しかし、独立でない場合、次の式が成り立つ。
$$
E(XY) = E(X)E(Y) + Cov(X, Y) \tag{b}
$$
独立でない場合、共分散の項がくっつくのだ。
式(b)を証明するために、共分散\( Cov(X, Y) \)の定義式(下の数式)から計算する。
$$
Cov(X, Y) = E[(X-E[X])(Y-E[Y])]
$$
以降、手書きで計算する。
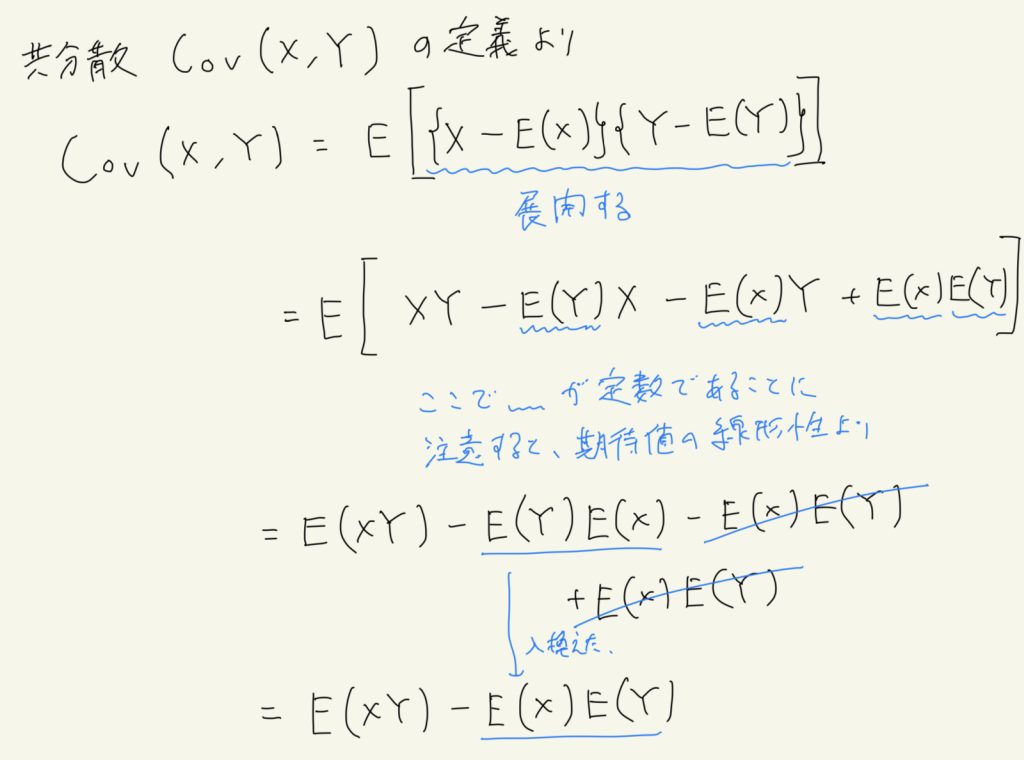
上の計算より、下の式が導ける。
$$
Cov(X, Y) = E(XY) – E(X)E(Y) \tag{c}
$$
E(XY)だけを左辺に持ってくると、式(b)が導ける。
$$
E(XY) = E(X)E(Y) + Cov(X, Y) \tag{b}
$$
(注意:期待値の計算を行ったE(X)などは変数ではなく、定数になることに注意)
参考にした本
通称「赤本」と呼ばれている有名な良書。








コメント