確率変数XとYについて、XとYが独立であれば和の分散は下のようになる。
$$
V(X + Y) = V(X) + V(Y)
$$
しかし、独立でない場合、共分散\( Cov(X, Y) \)が付き、下のようになる。
$$
V(X + Y) = V(X) + V(Y) + 2Cov(X, Y) \tag{a}
$$
共分散\( Cov(X, Y) \)は次のように定義され、XとYが同じ方向にゆらぐ(Xが平均より大きな値を取った時、Yも平均より大きな値を取る傾向がある)場合に\( Cov(X, Y) > 0 \)となり、XとYが逆方向にゆらぐ(Xが平均より大きな値を取った時、Yは平均より小さな値を取る傾向がある)場合\( Cov(X, Y) < 0 \)となる。
$$
Cov(X, Y) = E[(X – \mu_X)(Y – \mu_Y)]
$$
この記事では、式(a)で共分散の項が付く直感的な理由と証明を紹介する。
和の分散に共分散の項が付く直感的な理由
下の図のように、毎日タンクに液体Xと液体Yを入れるとします。液体Xと液体Yは完全に分離するとします。
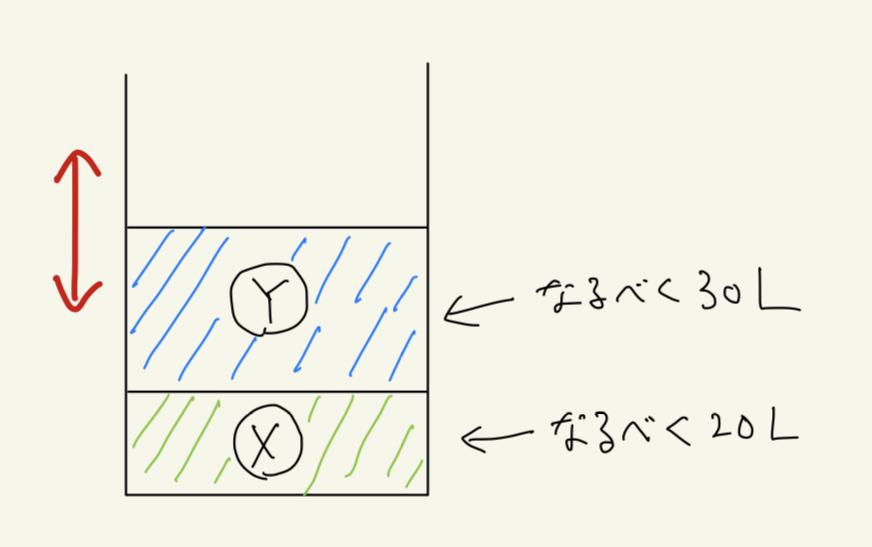
液体Xはなるべく20Lになるように入れ、液体Yはなるべく30L入れるようにします。
しかし、入れる量には誤差があるので、XとYをそれぞれの液体の入れる量だとすると、XとYは確率変数と考えることができます。
ここで\( V(X + Y) \)は、液体Xと液体Yの合わせた量が、日によってどの程度ゆらぐかを表します。
上の図で、赤い矢印で示した水位の日ごとのゆらぎがどれくらい大きいかを表しています。
XとYが同じ方向にゆらぐ場合、つまり共分散がプラスの場合、液体Xの量がたまたま20Lより多い日は液体Yの量も30Lより多い傾向があります。逆に、液体Xの量がたまたま20Lより少ない日は液体Yの量も30Lより少ない傾向があります。
そうなると、図の赤矢印で示した水位の振れ幅、つまり分散\( V(X+Y) \)は大きくなると想像が付きます。
XとYが逆方向にゆらぐ場合、つまり共分散がマイナスの場合、液体Xの量がたまたま20Lより多い日は液体Yの量は30Lより少ない傾向があります。逆に、液体Xの量がたまたま20Lより少ない日は液体Yの量は30Lより多い傾向があります。
この場合、一方が増えたとき、もう片方は減り、変化を打ち消すので、図の赤矢印で示した水位の振れ幅、つまり分散\( V(X+Y) \)は小さくなると想像が付きます。
和の分散の式の証明
確率変数の分散については下の記事で解説しているので、そちらも参照してほしい。
式(a)を分散の定義を元に計算していく。分散の定義は下のようになる。
$$
V(X) = E[(X – E[X])^2]
$$
以降、手書きで説明する。

参考にした本
通称「赤本」と呼ばれる有名な本。少し難しいが知識が網羅されている。







コメント