確率変数Xについて、その確率変数Xの期待値\( E(X) \)を知ることは重要だが、同じ程度に重要なのが分散\( V(X) \)である。
例えば、仮に「やみとも星人」というのが発見されたとして、新聞に「やみとも星人」の身長の平均(期待値)は300cmとだけ書かれていても、何かもっと知りたいのではないだろうか。
知りたいのは、「やみとも星人」の身長は300cmを平均として、どの程度ばらつくのか、ではないだろうか。
「やみとも星人」は皆クローンで身長はほとんど変わらない、だったり、地球人のようにそこそこのばらつきがあるのか。
このばらつきを表す指標が分散と標準偏差である。
分散の定義
分散\( V(X) \)の定義は次のようになる。
$$
V(X) = E[(X – \mu)^2] \tag{a}
$$
※期待値Eの演算の括弧は、中身と重複するので[ ]にした。
\( \mu = E(X) \)である。確率変数Xは変数であるが、期待値の演算後の\( E(X) \)は定数となる。
定数と分かりやすいように\( \mu \)という文字に置き換えた。
分かりにくいのであれば、下のように覚えても同じことだ。
$$
V(X) = E[(X – E[X])^2]
$$
式(a)の定義をさらに計算するときは、期待値の定義に従う必要がある。
期待値の定義については、次の記事を参考にしてください。
期待値の定義に従って分散の定義(a)を計算すると、確率変数Xが離散型と連続型の場合で次のようになる。
離散型の場合
$$
\begin{eqnarray}
V(X) &=& \displaystyle E[(X-\mu)^2] \\
&=& \displaystyle \sum_x (x – \mu)^2 f(x)
\end{eqnarray}
$$
連続型の場合
$$
\begin{eqnarray}
V(X) &=& E[(X – \mu)^2] \\
&=& \displaystyle \int_{-\infty}^{\infty} (x-\mu)^2 f(x) dx
\end{eqnarray}
$$
ただし、分散を期待値の定義通りに計算するのは手間が掛かるので、下の式変形が良く使われる。
必須の場面もあるので、ぜひ覚えておいてほしい。
細かい計算について補足したいので手書きで書く。
この公式を覚えるときは「分散は、2乗の平均、引く、平均の2乗」と覚えると良い。
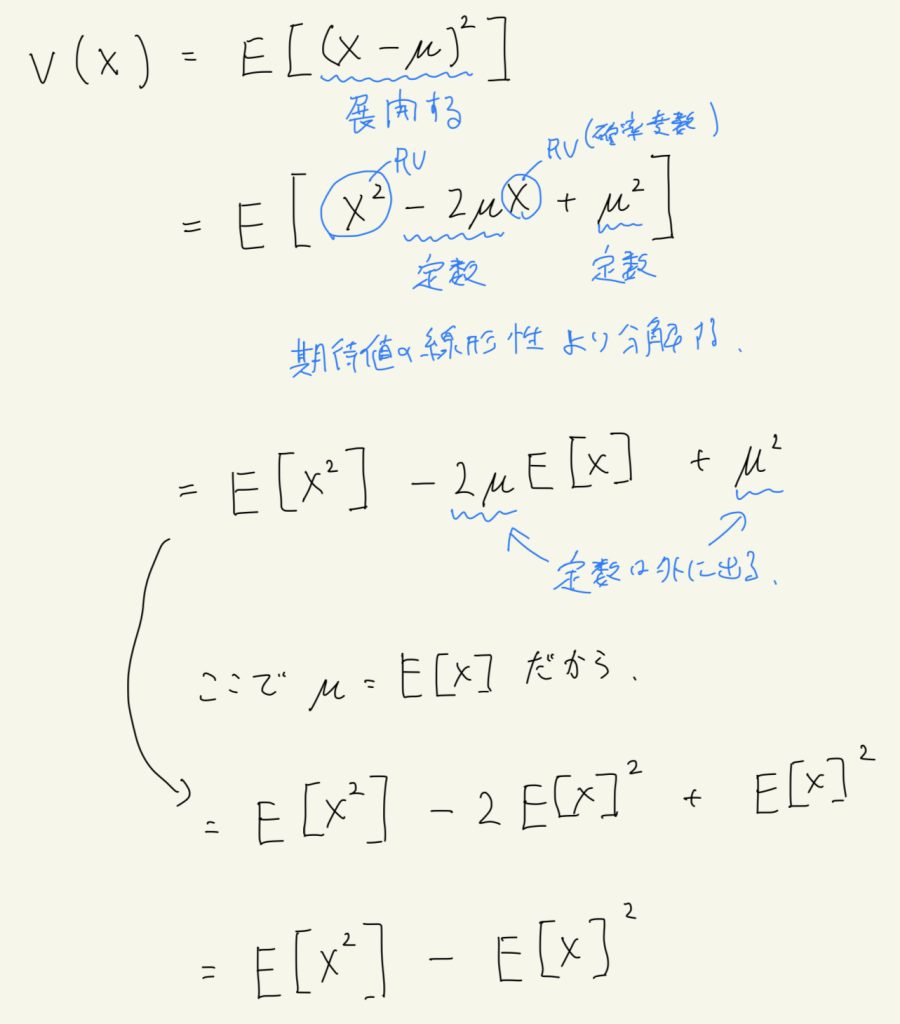
分散の性質
$$
V(c) = 0 \tag{a}
$$
$$
V(X + c) = V(X) \tag{b}
$$
$$
V(cX) = c^2 V(X) \tag{c}
$$
証明は下のようになる。
(a) \( V(c) = 0 \) の証明

(b) \( V(X + c) = V(X) \) の証明
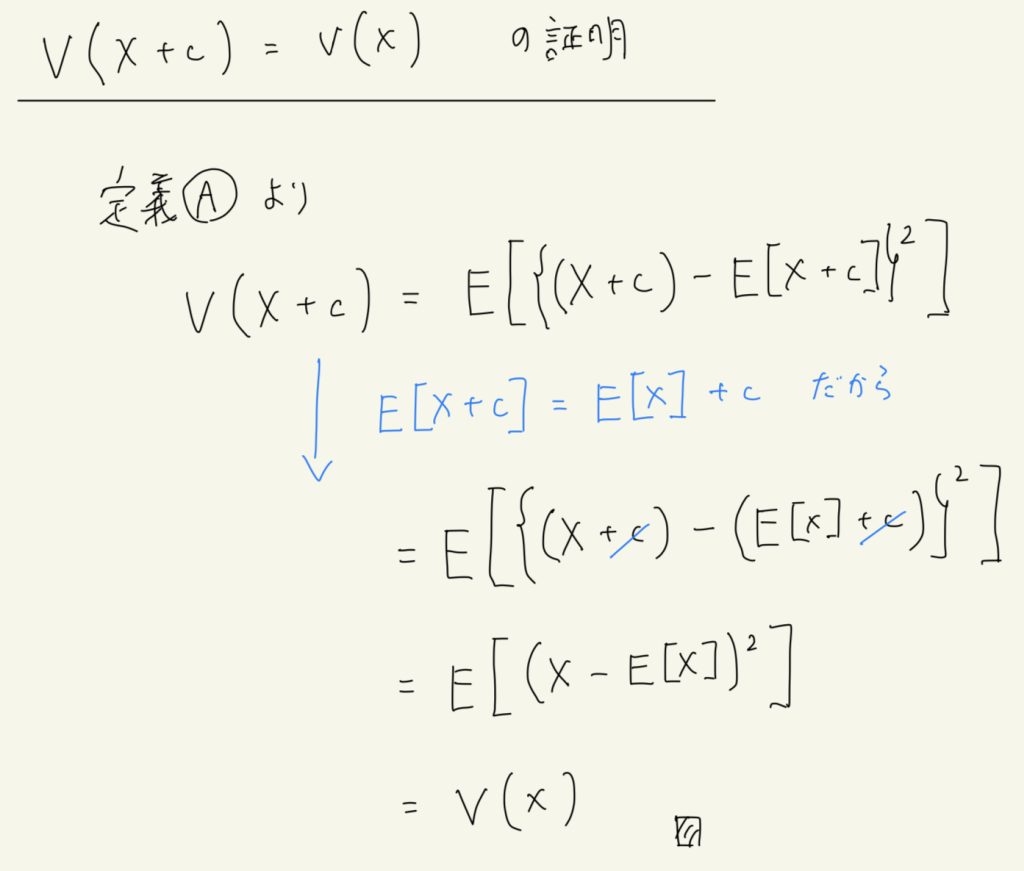
(c) \( V(cX) = c^2 V(X) \) の証明
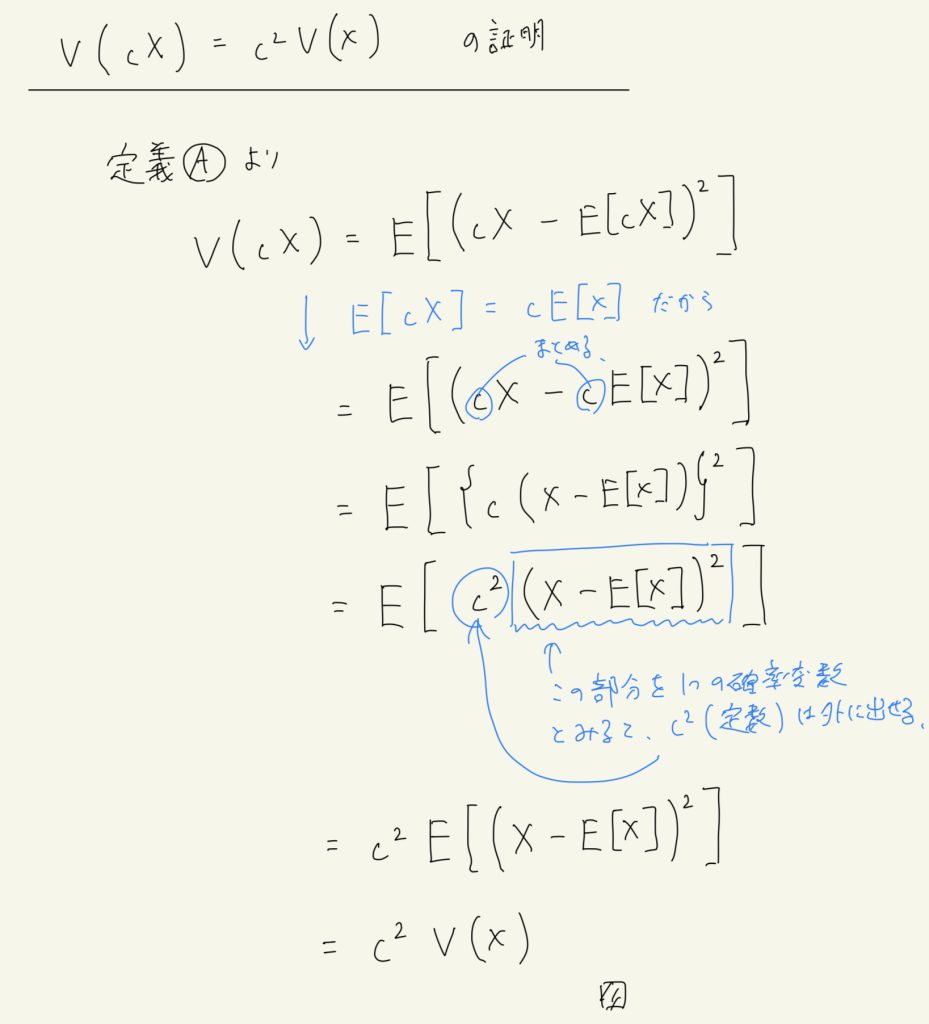
参考にした本
通称「赤本」と呼ばれる有名な本。少し難しいが知識が網羅されている。







コメント